Most of us are not color scientists, yet we encounter and work on colors all the time. Maybe you are buying a new TV, and the manufacture says that the TV covers “99% of P3”. “What does it mean?” you asked the clerk in the electronics store. “Oh it means it can display far more colors than the average TV,” the clerk replied, and they show you this diagram:

“Yes, but what does it really mean? Why does this…​thing…​look like this? Why are all the colors squeezed into the lower-left corner of the positive xy plane? What happened to the upper right half?”

“Ah well, because our TVs are really good! You don’t need to care about all the details; just enjoy the intense colors!”

Ok, maybe you are not buying the TV after all. Maybe you are just an innocent programmer. At some point you decide to build your own website, you have all the contents and the structures figured out, only the styling remains. Now you are trying to decide the color of the <a> element. The color #2e3735 looks promising.

But what is #2e3735, really? Why does it look like that? Who decided that this particular hex sequence should look like this yellow-green-ish color? Maybe you know that all colors on the web are defined in the sRGB space, but then what is sRGB? How is that defined? Is there an end to this chain of whys and hows?

This article tries to answer these questions.

Huge disclaimer: I am not a color scientist, either. I decided to dig into this topic, because I was that TV buyer, and I was that innocent programmer. And I still am. I still have a lot of gaps in the knowledge, so this article will probably contain mistakes. But I’ll do my best :→ Generally I will have references for important statements. The ones that do not are most likely just my unsophisticated understanding on the subject (aka. “trust me bro”, aka. “I guess”).

Although you almost never use this space directly, or encounter an image in XYZ space (the notable exception being DCP), you will see this space get referred to all the time. Most color spaces you will work in are practically defined by some transformation from the XYZ space, including the all-important sRGB. But before talking about the XYZ space, we need to briefly look at an extremely important concept: color matching functions.

Under normal lighting conditions, the cone cells in the retina take care of reproducing colors. There are three kinds of cone cell, with distinct responses to the spectrum. The responses are, of course, very hard (or impossible) to measure directly. So we have to find something close that is easier to measure, and that something is color matching functions.

[w&s]Imagine looking at a color produced by a monochromatic light, for example, orange. But as you know, some combination of red, green, and blue light (these are also monochromatic, but from now on I will only call the former monochromatic light “monochromatic” to prevent confusion) can also produce orange (red + green, with little to no blue). Therefore we can do an experiment, where we sweep the frequency range of visible light, and try to match the resulting color with combinations of red, green, and blue which are at fixed frequencies specified beforehand. In another word, with a monochromatic light of a given frequency, we can ask ourselves: can we mix the red, green, and blue light and adjust their intensities, so that the mix looks exactly the same color as the monochromatic light? The answer is usually “yes” (I will explain the “unusual” part later), and people have done this experiment. For each frequency of that monochromatic light, we can get three numbers, which are the intensities of the red, green, and blue light. After the experiment, we get three curves like these:

We will now call these three curves \(\bar{r}\), \(\bar{g}\), and \(\bar{b}\), respectively. They are functions of wavelength (or frequency). We will also call these the “color matching functions”, because…​ well…​ we get to these by matching colors. Using these functions as basis, a linear vector space can be constructed, with inner product

This is extremely useful, because now if we are given some kind of light, with a power distribution \(E(\lambda)\), we can just calculate how much intensity of the red, green, and blue light we need to mix, in order to match the color of that light:

In the equations above, R, G, and B are the intensity of the red, green, and blue light we need to mix in order to match the color of E, repsectively. This totally makes sense --- let us go back to our orange light. Using the equations above, we can figure out how we can get the color orange by mixing red, green, and blue light. Let us suppose the orange light is monochromatic at \(\lambda_0 = 600 \mathrm{nm}\). Its power distribution is then \(E = A \delta(\lambda - \lambda_0)\), where δ is the Dirac delta function, and A is just some arbitrary number denoting how strong the light is. Now we can just calculate R, G, and B by simply evaluating the integrals:

This is just the value of \(\bar{r}\) at 600 nm. Similarly \(G = A\bar{g}(\lambda_0)\), \(B = A\bar{b}(\lambda_0)\). Now we can just read on the color matching functions plot to get \(R \approx 0.31\), \(G \approx 0.07\), \(B \approx 0\), (assuming A = 1,) which basically just confirms our common sense that we can mix red light and green light to get orange. As you can see, once we have the color matching functions, we will never need to do the experiment of asking a human to match colors anymore, we can just do some calculation!

It is worth noting, however, that unlike the usual cartesian coordinate systems or the Hilbert space that has a similar definition of inner product, this space is not orthogonal, because \(\bar{r} \cdot \bar{g} \neq 0\), \(\bar{g} \cdot \bar{b} \neq 0\), \(\bar{b} \cdot \bar{r} \neq 0\). There is no physical law that puts such constraints. As a result, there is no guarantee that different power distributions (the \(E(\lambda)\) mentioned previously) would always produce different R, G, and B. In another word, given two lights with different power distribution \(E_1 \neq E_2\), it is entirely possible that

This may seem strange at first, but think about it --- this basically just means that lights with different power distribution can appear to be the same color to the human eye, which is, of course, completely natural! The experiment of matching colors would not be possible if that is not the case.

At this point, I must address the “elephant in the room” regarding the color matching functions. Recall that these functions are intensities of the red, green, and blue light. But some portion of \(\bar{r}\) is clearly negative! How on earth can one have a light with negative intensity?

Let us look at, for example, λ = 510 nm, where \(\bar{r} < 0\). This is a kind of green color. What happened here was that the participants of the experiment were unable to match this monochromatic light with any combination of the red, green (which is not 510 nm, by the way), and blue light. The only way they could make the match was to mix the 510 nm light with some red. And therefore in the resulting color matching functions, they had to take this red out, resulting a negative value.

Now maybe this makes sense to you, but it is undeniable that having negative values here is both inconvenient and weird. Therefore people have defined another set of color matching functions, which are just projectively transformed from the real color matching functions. They look like this:

Similar to the real color maching functions, these also form a linear vector space, with the same definition of inner product. The basis are called \(\bar{x}\), \(\bar{y}\), and \(\bar{z}\); and we also have

This is called the XYZ space. Togather with the real color matching functions, they form the CIE 1931 Standard Colorimetric System. Like I mentioned, the XYZ space is the starting point of practically all other color spaces.

We can go one step further, and simplify this still. We can define the so-called chromaticity x, y, and z as dimension-less variables

We can then let x and y form a 2-dimentional space (z is not independent anymore). With this we can do another experiment: given a monochromatic light with some frequency, we can calculate the value of x and y, and put a point on the xy plane. If we sweep the whole spectrum, we should end up with a curve. What does it look like? The answer is the following graph:

This is called the chromaticity line. Imagine drawing a straight line connecting the two ends of this curve; this line is called the line of purple, because all colors on this line look like some kind of purple. This also closes the chromaticity line. All the possible colors viewable by human are enclosed within this region. (I am not sure exactly why though. Is this mathematical, physical, or biological? I have not found an answer yet in [w&s]. There is a Wikipedia entry, but I am not fully convinced.)

An RGB color space is spanned by a set of red, green, and blue. The definition of those colors is specific to each RGB space. Fig. [The RGB color space] shows a linear RGB space “embedded” in the xyz space.

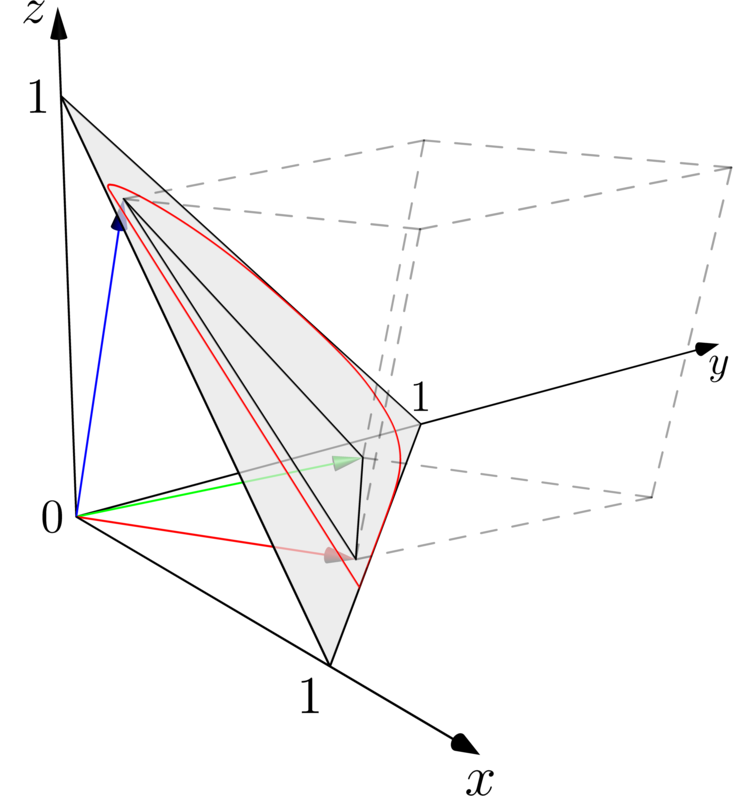
The red, green, and blue vector coincides with those of sRGB and Rec.709 under “white point D65”. The big grey triangle is the \(x+y+z = 1\) plane. The chromaticity line is drawn as the red curve. If one projects it onto the x-y plane, one recovers the curve in fig. [[img-domain]]. The RGB vectors defines a triangle (shown in black, the smaller one) on the \(x+y+z = 1\) plane; this is the gamut of the RGB color space. The light grey dashed lines visualize the entirety of the linearized version of the RGB color space, inside which are all the colors that can be expressed with this linearized RGB color space.